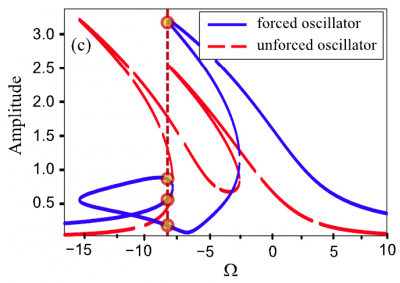
We discuss a similarity between resonant oscillations in two nonlinear systems; namely, a chain
of coupled Duffing oscillators and a bilayer fish-scale metamaterial. In such systems two
different resonant states arise which differ in their spectral lines. The spectral line of the first
resonant state has a Lorentzian form, whereas the second one has a Fano form. This difference
leads to a specific nonlinear response of the systems which manifests itself in the appearance of
closed loops in spectral lines and bending and overlapping of resonant curves. Conditions for
achieving bistability and multistability are determined.